High frequencies in an acceleration signal

It is often argued that high frequency components in an acceleration signal should be omitted. The motivation given is that these high frequencies are a consequence of machine noise or vibrations, or at least not human. With this comes the assumption that human movement can only cause low frequency components. Here, the division line between low- and high frequencies varies across studies from 5 to 20 Hertz.

Intermezzo – What do we mean by ‘frequencies in an acceleration signal’?

Joseph Fourier showed that a time series can be described as the combination of multiple sine waves, each with their own frequency characteristic. A periodogram is a visualisation of the contribution of all those sines to the total variance in a time series. The frequencies are shown on the horizontal axis and their contribution to the variance is displayed on the vertical axis.

Are high frequencies truly just noise?

At first, the idea that high frequencies are not caused by human movement sounds plausible: A washing machine at top speed rotates at around 23 Hertz. Surely our body would not be capable of producing that kind of rotations.

Nevertheless, very little empirical research has been done to support the idea that all high frequencies are redundant. To me it does not feel satisfying to embrace this widespread belief without having clear evidence for it. For example, it would be helpful to know the relative contribution of human movement, machine noise, and non-human vibrations to the frequency content of a signal. Also, it would be good to know whether these contributions vary across the frequency spectrum. Such insights would help to make an informed decision on what frequency filter to use, if any.

To gain a better understanding I did the following short experiments together with my project partners in Regensburg:

Accelerometer data from walking and non-wear

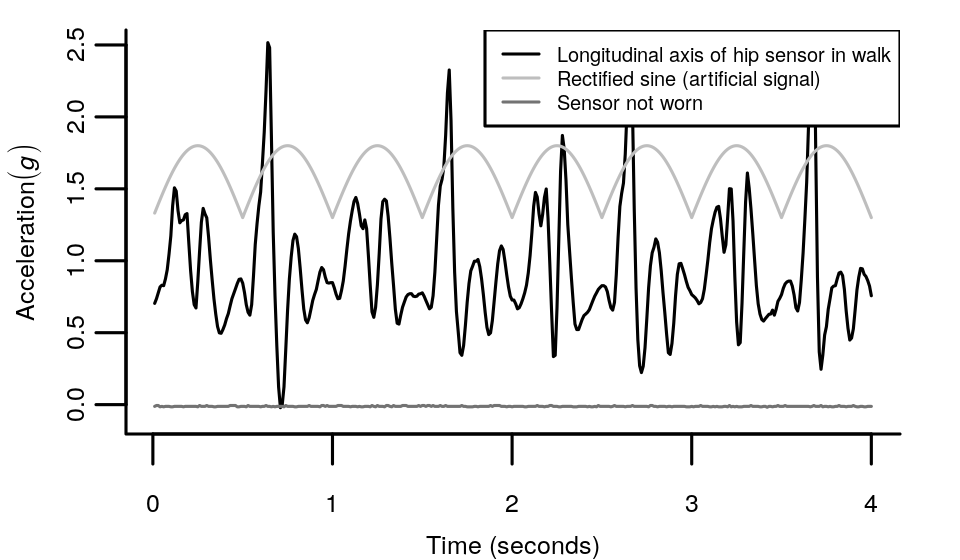
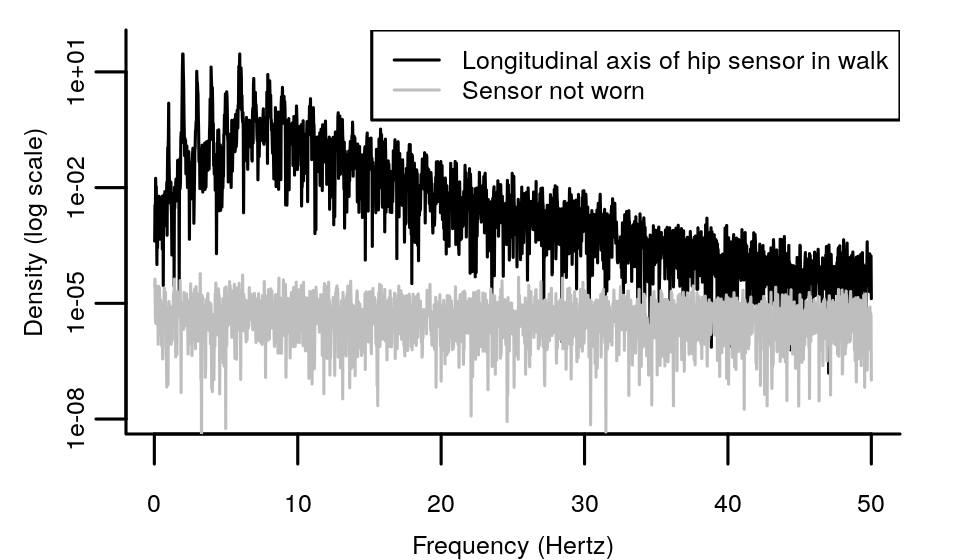
The acceleration signal was collected with a hip-worn accelerometer in walking. This tri-axial accelerometer was configured to collect data at 100 Hertz. Additionally, I have a recording of that same accelerometer when it was lying still on a table (not worn). Both signals have a length of 45 seconds and I only look at the vertical (longitudinal) signal. The periodograms show that the frequency density is consistently higher for walking than when the accelerometer is not worn. Not just during the low frequencies below 10 Hertz, but all the way up to 50 Hertz. This indicates that the high frequencies in the signal for walking are not simply explained by a natural level of noise seen when the sensor is not worn.

Enhancing theoretical understanding with artificial data

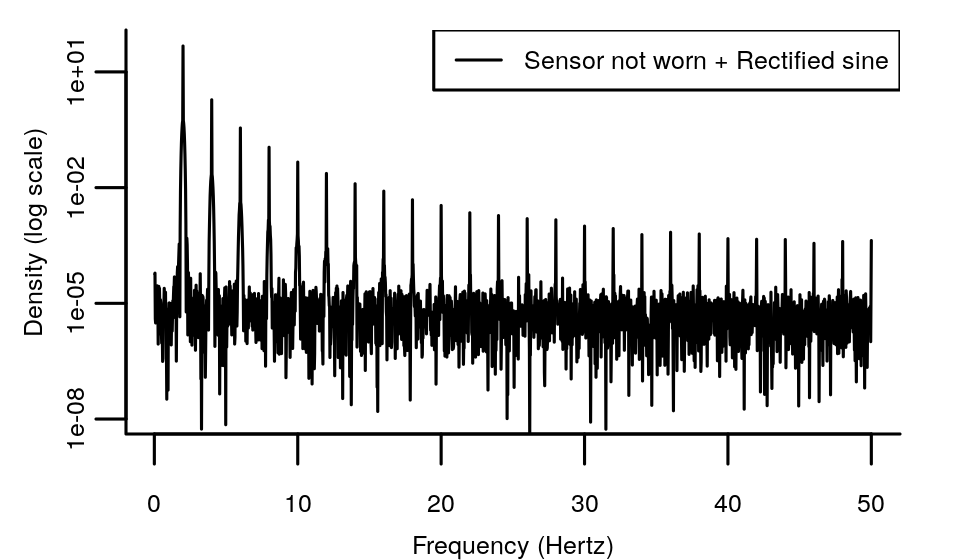
I complemented these accelerometer experiments with an artificial signal. The artificial signal is a rectified 1 Hertz sine wave, which looks like a pendulum motion. Pendulum motions are often used as a model for human movement where smooth rotations are interrupted by abrupt changes in movement direction. Next, I sum this artificial signal with the experimental non-wear data (discussed above). The resulting periodogram shows not only a peak for the resulting 2 Hertz frequency of the pendulum, but also it’s harmonics at higher frequencies. Harmonics are a natural consequence of waves that do not have a perfect sine shape. In sound, the specific shape of the wave is what gives our voice and musical instruments their characteristic sound. In acceleration signals the harmonics give the wave it’s movement specific shape.

Interpretation

The periodogram of the artificial signal looks suspiciously similar to what we see in the periodogram of the signal for walking. The peaks in both have a gradual decline towards the top frequency.

Based on this it would seem likely that higher frequencies in an acceleration signal are not only caused by machine noise but also by the harmonics of movement. In fact, the contribution of the harmonics is much larger than the contribution of signal noise in this little experiment. Further, the experiment shows that even a simple 2 Hertz pendulum movement can produce high frequency components. However, it is not a single human body joint that is rotating at these high frequencies. It is the combined impact of multiple joint movements and the interaction of the human body segments with each other and with the environment (floor in this case) that causes the pendulum shape. The pendulum shape in turn produces a broad frequency profile. If we would filter out these harmonics in the signal, we would lose the detailed representation of body movement in the original signal.

How about sensor vibrations?

The other explanation offered for high frequencies is that they represent vibrations of the accelerometer relative to the human body. For example, as a result of loose attachment with an elastic strap or because of skin movement relative to the underlying bones. In general, when objects vibrate they tend to vibrate at their, so called, eigenfrequency. However, when we look at the periodogram of walking we see a homogeneous increase in density of all frequencies. If the high frequencies would only be caused by a vibrations then we would expect to see an increase near the eigenfrequency or a set of eigenfrequencies for those vibrations.

Conclusion

In conclusion, high frequencies in an acceleration signal can represent body movement. Therefore, filtering out high frequencies may not necessarily be a good thing. Not filtering the signal will preserve the detailed representation of the movement. Additional advantages of not filtering are that it is computationally faster, and that signal processing is potentially easier to reproduce as there are less computational steps.

In the specific use case of assessing human daily physical activity I recommend the following:

• Do not filter out the high frequencies unless there is clear evidence that filtering gives better estimates of physical activity. To my knowledge there are no studies that show the added value of filtering.
• Only consider filtering out high frequencies if data comparability between accelerometer brands/generations is critical to your research question. Accelerometer brands and generations can have different sensitivities to human body acceleration. By filtering out high frequencies you create a less precise but potentially more comparable acceleration signal.

The exploration described in this blog post is part of the project I am doing for the University of Regensburg, Germany.